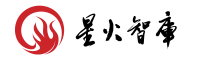遥遥领先：南北朝最强大脑有多神？

在月球背面的诸多环形山中，有5座以中国古代天文学家命名，分别是祖冲之、郭守敬、张衡、石申和万户环形山。在5座环形山中，郭、张、石、万4座都是1970年被国际天文联合会正式批准的，独有位于月纬17.16°N，月经145.16°E的祖冲之环形山早了9年，1961年就获得了国际天文学会的认可。

提起祖冲之，也许第一时间想到的是他在公元5世纪作出的杰出数学成就–也就是众所周知的圆周率π精确近似值以及约、密率。

但人们还忽略了，他不仅是名出色的数学家，更是一位在历法上作出不灭贡献的天文学家。

祖冲之，字文远，祖上是北方范阳（今河北涞水县）人，他本人则是土生土长的江南人。北方的范阳祖氏跑到南方生根，自然是因为西晋末永嘉大乱。

祖冲之像。祖冲之是南朝宋、齐时代杰出的数学家、天文学家。他最为家喻户晓的成就为算出圆周率π精确近似值并给出约、密率，其结果领先世界千年之久。除此之外，他还是杰出的天文学家，编制了《大明历》

晋元熙二年、刘宋永初元年（420），刘裕灭东晋建立刘宋，祖家也像大多数人一样继续在朝廷任职。祖冲之祖父祖昌担任过将作大匠（梁武帝时改名大匠卿），品秩为中二千石，负责朝廷的土木工程；父亲祖朔之为奉朝请，为南朝安置闲散官的职务。正史中祖台之本传就只有一句话，祖昌和祖朔之甚至无传，但让人诧异的是，虽然父祖默默无闻，祖冲之却在刘宋第四任皇帝孝武帝刘骏在位时翻了身，进入世人的视野中。

祖冲之生于元嘉六年（429），比刘骏大一岁，史书中并未记载两人早期有什么瓜葛，但刘骏即位后，立即让祖冲之”直华林学省”，并”赐宅宇车服”（《南齐书·祖冲之传》）。《宋书》中没有”华林学省”的记载，但频频提到华林园，武帝、孝武帝多次在此亲自听取诉讼，少帝被弑前在华林园摆摊，可见是刘宋皇帝常去的一处园子，推测”直华林学省”为在华林园办公的皇帝近侍应属合理。不仅如此，大明五年（461），祖冲之首次出仕（”释褐”）就被任命为南徐州刺史刘子鸾的从事、公府参军更值得世人深思：刘子鸾为刘骏最宠爱的儿子，只要父亲看到什么好东西，”莫不入子鸾之府”，此外以皇子领大郡是刘宋压服地方豪族的惯例，为了辅助这些不谙世事的皇子，往往会给他配属精明能干的帝王心腹作为幕僚。大明五年时刘子鸾才5岁，遥领可能性更大，祖冲之到底是在南徐州处理公务还是在京城刘子鸾身边虽不可知，但能厕身皇帝托付爱子的近臣行列，可见他同刘骏关系远较旁人想象得密切。

大约在此时期，得到皇帝充分信任的祖冲之才能作出一项牵涉学术外甚多的重大天文改革–修改传统历法，推出《大明历》。

美国月球轨道器5号（Lunar Orbiter 5）拍摄到的祖冲之环形山，该环形山位于月纬17.16° N，月经145.16° E，直径28.3公里，深度1.98公里。该环形山最早由1959年升空的苏联月球3号卫星拍摄到，苏联科学院在征求中方意见后将其命名为祖冲之环形山

创造出灿烂农业文明的中华先民出于生产需要，很早就对历法产生了浓厚的兴趣，而且经过长期的对日月运行规律的观察和总结，他们发展出了一套较为罕见的阴阳历结合的历法，即以一次月圆（或月缺）到下次月圆（或月缺）为基准定月（朔望月），而以当年冬至到次年冬至为基准定年（回归年）。这么定的好处在于以朔望月定月，抬头即可确定时间，方便确定；以回归年定年，每年季节大致相同，方便生产。

然而，朔望月实际是月球绕地周期时长，回归年是地球绕太阳时长，两者并不能整除，每月按大小月分别为30或29天，算下来12月为354天，但回归年共365.25天，两者有11天左右的差距。为解决此问题，古代天文历法家采用置闰法加以补齐，也就是每隔两三年就多加一个”闰月”，由此又衍生出一个新问题：那么到底该多少年置一闰月？

解决方案早在先秦时期就被提出，人们在实践中发现19个回归年的时长同235个朔望月差不多相当，便在正常19年的228个月外另加7个闰月敉平差距。由于古人将19年称为一”章岁”，19年7闰也就被称为”章岁法”。从汉代开始流行的”四分历”，正是基于”章岁法”制定的。

很显然，”章岁法”只是一种近似，时间一长误差就会越来越大，到南北朝时人们已然发现，”章岁法”虽然能将日子合上，但每月时间却同当月原应有的季节产生了偏差，对一个需要按月份节气进行农业生产安排的国家来说，这无疑是天大的噩耗，修正历法的需求也变得迫切起来。

终于，祖冲之在经过反复计算后，认为每年实际为365.24281481日，而现代天文学所测一年为365.24219879日，误差只有65万分之一，约50秒。因而提出改为391年置144闰月。

《南齐书·祖冲之传》，祖冲之生于南朝刘宋文帝元嘉六年（429），卒于南齐永元二年（500），因而被列入《南齐书》列传。不过，他生平心血所编制的《大明历》在宋齐两朝因为种种缘故都未能付诸实施，直到他去世10年后梁武帝天监九年（510）方才施行

祖冲之为什么能将回归年确定得如此精确？最主要的原因，就是他引入了当时最先进天文发现成果-东晋天文学家虞喜确认的赤道岁差。

所谓赤道岁差，是一种地球自转轴运动引起的春分点位移现象。

祖冲之铜像。祖冲之不仅是杰出的数学家，同时也是在历法上作出不灭贡献的天文学家。他在《大明历》中引入了赤道岁差，还准确计算出交点月值（月亮两次经过黄道与白道交点时长），推算出木星公转周期，确定了水星、金星运转一周所需时间，成就卓著

制定准确的历法，使用岁差确定每年时长是一个方面，另一方面自然就是确定冬至点时刻。中国古代历法向来以冬至点为回归年开始，确定具体冬至点时刻也成为历法的重中之重。在相当长的一段时间内，古人测定冬至的方法很粗糙，就是将一年当中正午日影最长之日定为冬至日，误差能以天计。从西汉开始，天文学家意识到精度需要从天提高到具体时刻，开始尝试寻找具体的冬至时刻点，到何承天时通过改进测量手段，已经将精度提高到50刻左右。然而，正是在这些测量手段之上，祖冲之通过一个极为巧妙的数学处理方法，又将冬至点精度提高了一大截。

祖冲之通过数学方法将难以测量的时间实际转换为几何计算，从而大大减小了误差。按他的方法，人们根本不用连续观测，只需在冬至日前后观测即可，考虑到此时只是公元5世纪，他的数学思维实在让人叹服。事实上，在祖冲之编制的《大明历》中处处都有精妙的计算，他不仅准确计算了交点月值（月亮两次经过黄道与白道交点时长）为27.21223日，同现代观测相差只有百万分之一，使得推算月食更为精确–《大明历》能准确推算出元嘉十三年（436）到大明三年（459）中4次日食。除此之外，祖冲之还推算出木星公转周期为11.858年（现代测定11.862年），确定了水星、金星运转一周所需时间，都同现代天文观测相近，要不是因为其他缘由遮掩，光凭一本《大明历》说他是伟大数学家和天文学家都已足矣。

不过无需遗憾，因为遮掩历法中数学才华不是别的，正是他在数学上的另一项伟大成果–计算出精确圆周率，提出了约率（22/7）和密率（355/113）。

圆周长和半径之比π到底是多少？这不仅是人们研究天文必然遇到，更是他们只要进行生产生活就会遇到的问题。人类最早有关圆周率的记载于约公元前16世纪的埃及莱因德数学纸草书（Rhind Mathematical Papyrus），算得圆周率为3.1605。当时古埃及人常用经验公式确定π值，方法也很简单：他们将谷子摆放在圆周和直径上，通过计算谷子比例可以得到π的近似值。

中国古代最早的数学著作之一，约成书于西汉末的《周髀算经》提到”圆径一二周三”，显然是将π值定为3，即古人所称的”古率”，虽然只是π很粗略的近似值，但以当时的数学发展水平，没有办法算出更好的值，因而在成书于东汉初的《九章算术》中也都在使用”古率”。

刘徽像，出自纪念邮票《中国古代科学家第四组》。刘徽（约250—？）为魏晋数学家，他的《九章算术注》和《海岛算经》为我国最宝贵的数学遗产。他在《九章算术注》中具体介绍了用古典几何方法求圆周率的具体过程——割圆术

中国人得出较为精确的π值始于西汉末新莽时期。

新莽嘉量，又名律嘉量斛，通高25.6厘米，现藏台北故宫博物院。该青铜量具将五种量具融于一体，“其上为斛、其下为斗，左耳为升，右耳为合，合下为龠”，背面铭文则说明了斛的具体尺寸，从中可推算出当时制作者所使用的π值约为 3.1547

此后东汉张衡、蔡邕也都是使用经验公式给出了近似π值，张衡认为等于3.1622（10开方）；蔡邕认为等于25/8，直到魏晋之际，数学家刘徽在给《九章算术》做注时，才第一次给出求圆周率的几何方法–割圆术。

阿基米德割圆术示意图，他通过同时构造圆内接和外切正多边形，然后计算其周长以取得周长近似值，重复该步骤求得圆周率约为3.1409<π<3.1429。阿基米德的算法需要同时计算内接和外切正多边形，计算量较割圆术大不少，同时由于割圆术利用“差幂”的思路接近数值分析中“最小二乘法”，数值精度会更高

祖冲之正是在刘徽等人的基础上，同他儿子祖暅（亦有记载为祖暅之）将圆周率推到一个新高峰，精确到小数点后7位。

尽管他使用的仍然是几何方法，但国外要直到15世纪才由中亚数学家阿尔卡西（al-Kashi）打破了他的记录，计算到小数点后14位，更为精确的计算则要等到18世纪中叶后，西方数学家掌握无穷级数、积分、幂级数展开等近代数学工具才得以实现。

此外，不容忽略的是，祖冲之给出了简便而又精度甚高的约率和密率，约率大概是根据刘徽给出π近似值157/50而来，通过解不定方程，得到第一组解即为22/7，而密率大约为祖冲之独创，但后世已不知道他是如何求出此解，只能猜测可能是使用了何承天的”调日法”（数值逼近的内插法），或是使用了连分数法求最佳渐进分数，但不管是何种方法，西方都直到1573年才由德国数学家重新算出。以是而言，祖冲之对圆周率的计算领先世界千年之久。

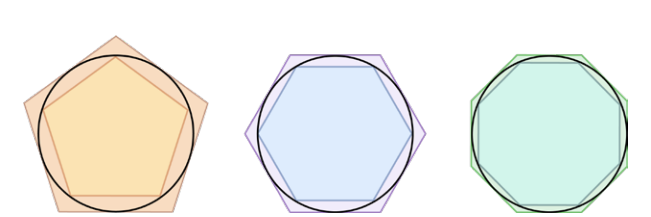
祖暅原理示意图。左右两堆硬币满足同高的立体等高处的截面积相等的条件，因而体积相等，即所谓“幂势既同，则积不容异”。图中直观地表现了此原理，但严格数学证明需要应用高等数学中的定积分

无论是《大明历》还是圆周率，祖冲之的成就可谓震古烁今，而他取得成就最根本缘由，无疑就是超人的数学思维。然而让后人遗憾的是，记载他和祖暅数学思想的《缀术》在唐代就失传，以至于后世根本无从了解祖氏父子的计算方法，只能从他人转述的残片中领略两人风采。比如，祖暅曾在《缀术》中提到”幂势既同，则积不容异”，意思是两个同高的立体，如在等高处的截面积相等，则体积相等。或者说，介于两个平行平面之间的两个立体，被任一平行于这两个平面的平面所截，如果两个截面的面积相等，则这两个立体的体积相等。祖暅原理直到17世纪才被西方学者卡瓦列里（Cavalieri）发现，而在中国早被祖氏父子熟练用于求出牟合方盖体积，进而算出球体积。

事实上，祖暅原理的证明需要用到定积分，在当时需要相当抽象的立体几何能力才能理解，由此也可想见《缀术》难度之大。唐高宗时，此书被列入《算术十经》，为国子监数学教材之一，但专研《缀术》的学习年限为四年，是《算术十经》中最长的一种。《缀术》之抽象难懂甚至还引发一桩公案，《缉古算经》的作者、数学家王孝通在唐高祖时为历算博士、太史丞，公然批评《缀术》”全错不通”，结果太宗群臣编写组就在《隋书·律历志》暗中发出嘲笑：“（《缀术》）学官莫能究其深奥，是以废而不理”。

好在，祖冲之和他儿子光辉的学术成果远比一切命运打击都更为长久。千年以降，祖冲之之名不仅没有被人遗忘，还走出国门，登上了月球。

参考文献：

金开诚、郭蕊《数学泰斗祖冲之》

魏晓妮《历史上对圆周率的探索》

本文摘编自《国家人文历史》2023年3月上，原标题为《不只算出了精确π近似值 祖冲之：南北朝最强大脑》，有删节